HEAPSORT

Se da un vector de numere intregi. Sa se ordoneze crescator valorile din vector.

Fisier de intrare: sort.in
Linia 1: n - numarul de elemente din vector
Linia 2: A1 - elementul 1 din vector
...
Linia n+1: An - elementul n din vector

Fisier de iesire: sort.out
Linia 1: S1 ... Sn
unde S este sirul A sortat crescator

Restrictii
-30000<=A1, ..., An<=30000
1<=n<=30000

Analiza problemei

Am studiat mai multi algoritmi de sortare. Cel mai cunoscut dintre acestia este BubbleSort, care este studiat primul in clasa a IX-a. Dupa cum se stie, complexitatea cu care acesta sorteaza datele de intrare este de O(n^2) in cel mai defavorabil caz.

Alti algoritmi simpli studiati in clasa a IX-a care ruleaza in aceeasi complexitate sunt: InsertSort (sortarea prin inserare), SelectSort (sortarea prin selectarea minimului/maximului). Cel mai avantajos algoritm de sortare este MathSort (sortare prin numarare) care ruleaza in O[n+D], unde D este dimensiunea spatiului de valori. Din pacate acest algoritm poate fi aplicat pentru domenii reduse de valori.

Ulterior, au fost studiati si alti algoritmi de sortare mai eficienti: QuickSort (sortare rapida) care in medie are complexitatea O(n log n) dar in cazul cel mai defavorabil ajunge la O(n^2), MergeSort ( sortare prin interclasare ) care are complexitatea O(n log n) dar necesita o structura de date suplimentara care ar putea constitui o problema in ceea ce priveste spatiul disponibil.

Pentru o complexitate mai buna (sau cel putin la fel de buna) si fara a necesita structuri de date suplimentare putem folosi algoritmul de sortare cu heap-uri, denumit si HeapSort. Astfel, datele din vectorul de intrare sunt organizate initial sub forma unui heap. La fiecare pas se extrage radacina (fiind mutata eventual pe pozitia care se elibereaza in procesul extragerii) si se reorganizeaza sub forma de heap vectorul obtinut printr-o operatie de combinare de heap-uri. Complexitatea acestui algoritm va fi O(n log n). Procedura de organizare a vectorului in heap a fost analizata la capitolul Creare Heap: O(n). La fiecare pas se reorganizeaza heap-ul in complexitate O(log n). Astfel, algoritmul propriu-zis ruleaza in complexitate O(n log n).
Pentru o intelegere mai buna a acestui algoritm puteti urmari o simulare animata.

SIMULARE

ARBORE PARTIAL DE COST MINIM

Fie G=(V, U) un graf neorientat si c: U->R+ o functie prin care se asociaza fiecarei muchii o valoare reala pozitiva numita costul muchiei. Sa se determine un arbore partial (graf partial conex si aciclic) de cost minim al grafului G. Prin costul unui arbore se intelege suma costurilor muchiilor din arbore.

Fisier de intrare: apm.in
Linia 1: n m - numarul de noduri, respectiv numarul de muchii din graf
Linia 2: X1 Y1 C1- exista muchie intre nodurile X1 si Y1 de cost C1;
...
Linia m+1: Xm Ym C1- exista muchie intre nodurile Xm si Ym de cost Cm;

Fisier de iesire: apm.out
Linia 1: S1 D1
...
Linia n-1: S(n-1) D(n-1)
unde Si Di reprezinta descrierea muchiei i din arbore.

Analiza problemei

Pentru a determina arborele partial de cost minim al unui graf au fost studiati doi algoritmi fundamentali: algoritmul lui Prim si algoritmul lui Kruskal. Vom analiza complexitatea celui de-al doilea algoritm si modul in care il putem optimiza utilizand un heap.
Algoritmul lui Kruskal implica selectarea de n-1 ori (unde n reprezinta numarul de varfuri din graf) a unei muchii de cost minim, care nu formeaza cicluri cu cele deja selectate. O prima idee ar fi sa sortam muchiile dupa cost, apoi sa selectam in ordine n-1 muchii care nu formeaza cicluri. Complexitatea algoritmului va fi egala cu complexitatea algoritmului de sortare, deci in cazul unui algoritm de sortare eficient O(m log m) (unde cu m am notat numarul de muchii din graf, care poate fi de ordinul lui n^2), la care se adauga complexitatea algoritmului de construire a arborelui partial (O(n)*numarul de operatii necesare pentru a retine evidenta componentelor conexe). Evidenta componentelor conexe este necesara pentru a testa daca o muchie formeaza sau nu cicluri cu cele deja selectate.
O prima optimizare a acestui algoritm se poate realiza observand ca nu este necesar sa sortam muchiile. Este necesara o structura de date care sa ne permita sa selectam eficient n-1 muchii de cost minim. Pentru aceasta, vom organiza muchiile ca un heap (complexitatea acestei operatii fiind O(m)). In etapa de constructie a arborelui partial vom extrage succesiv muchii de cost minim, complexitatea operatiei de extragere fiind O(log m). Observati ca facand aceasta optimizare am redus deja complexitatea algoritmului la O(m)+O(n log m) * nr de operatii necesare pentru a retine evidenta componentelor conexe.
Observati ca nu am determinat complexitatea operatiei de evidenta a componentelor conexe. Aceasta este O(n) daca retinem intr-un vector evidenta componentelor conexe sau O(log n) daca retinem evidenta componentelor conexe cu ajutorul unor arbori, implementand eficient operatiile union-find.

Implementarea algoritmului Kruskal cu organizarea muchiilor ca heap. Vizualizare sursa. Salvare sursa.

APLICATII PROPUSE

1. Fie G=(V, U) un graf neorientat si c: U->R+ o functie prin care se asociaza fiecarei muchii o valoare reala pozitiva numita costul muchiei. Fie x0 si y0 doua varfuri din graf. Sa se determine drumul de cost minim dintre cele doua varfuri date. Prin costul unui drum se intelege suma costurilor muchiilor ce apartin drumului.

Fisier de intrare: drum.in
Linia 1: n m - numarul de noduri, respectiv numarul de muchii din graf
Linia 2: X1 Y1 C1- exista muchie intre nodurile X1 si Y1 de cost C1;
...
Linia m+1: Xm Ym Cm- exista muchie intre nodurile Xm si Ym de cost Cm;
Linia m+2: S D - cele doua varfuri pentru care trebuie calculat drumul minim.

Fisier de iesire: drum.out
Linia 1: C - costul drumului minim.

Indicatie: Folositi algoritmul lui Dijkstra optimizand cautarea valorii minime la un anumit pas. Pentru a putea extrage minimul in timp [log n] organizati vectorul de valori temporare ca un heap.

 

2. Se da un sir de numere intregi si doua numere X si Y. Sa se determine subsecventa de suma maxima a carei lungime se afla in intervalul [X,Y].

Fisier de intrare: secv.in
Linia 1: n - numarul de elemente din sir
Linia 2: A1 - elementul 1 din sir
...
Linia n+1 - An - elementul n din sir.

Fisier de iesire: secv.out
Linia 1: Smax - Suma maxima ceruta.

Indicatie: Calculati sumele Si = A1+A2+...+Ai. Observam ca suma oricarei subsecvente poate fi scrisa ca o diferenta intre doua elemente din S (Exemplu: Suma subsecventei [2..5] = S5-S1). La pasul i consideram ca trebuie o subsecventa care sa se termine in i si care are suma maxima. Pentru a calcula maximul putem alege Y-X+1 subsecvente diferite. Organizati sumele acestor subsecvente intr-un heap pentru extragerea maximului.

3. Urgenta (Olimpiada Judeteana de informatica 2002)

Autoritatile dintr-o zona de munte intentioneaza sa stabileasca un plan de urgenta, pentru a reactiona mai eficient la frecventele calamitati naturale din zona. In acest scop au identificat n puncte de interes strategic si le-au numerotat distinct de la 1 la n. Punctele de interes strategic sunt conectate prin m cai de acces avand prioritati in functie de importanta. Intre oricare doua puncte de interes strategic exista cel mult o cale de acces ce poate fi parcursa in ambele sensuri si cel putin un drum (format din una sau mai multe cai de acces) ce le conecteaza.
In cazul unei calamitati unele cai de acces pot fi temporar intrerupte si astfel intre anumite puncte de interes nu mai exista legatura. Ca urmare, pot exista mai multe grupuri de puncte in asa fel incat intre oricare doua puncte din acelasi grup sa existe macar un drum si intre oricare doua puncte din grupuri diferite sa nu existe drum.
Autoritatile estimeaza gravitatea unei calamitati ca fiind suma prioritatilor cailor de acces distruse de aceasta si doresc sa determine un scenariu de gravitate maxima, in care punctele de interes strategic sa fie impartite intr-un numar de k grupuri.

Fisier de intrare: urgenta.in
n m k
i1 j1 P1 - intre punctele i1 si j1 exista cale de acces de prioritate P1
i2 j2 P2 - intre punctele i2 si j2 exista cale de acces de prioritate P2
...
im jm Pm - intre punctele im si jm exista cale de acces de prioritate Pm

Fisier de iesire: urgenta.out
gravmax - gravitatea maxima
C - numarul de cai de acces intrerupte de calamitate
k1 h1 - intre punctele k1 si h1 a fost intrerupta calea de acces
k2 h2 - intre punctele k2 si h2 a fost intrerupta calea de acces
...
kC hC - intre punctele kC si hC a fost intrerupta calea de acces

Restrictii si precizari
- 0<n<256
- n-2<m<32285
- 0<k<n+1
- prioritatile cailor de acces sunt intregi strict pozitivi mai mici decat 256
- un grup de puncte poate contine intre 1 si n puncte inclusiv
- daca exista mai multe solutii, programul va determina una singura.
- timp maxim de executie: 1 secunda / test

Exemplu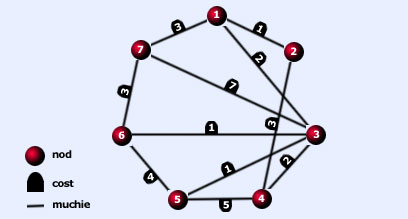